Chapter 1: Exposition
When you hear a beautiful work of music, what makes it pleasing? How do the different frequencies of music combine to create the overall harmony? Musical notes, like all other sounds, are vibrations of molecules in the air. These molecules vibrate at certain frequencies, which gives rise to the pitch of the musical note.
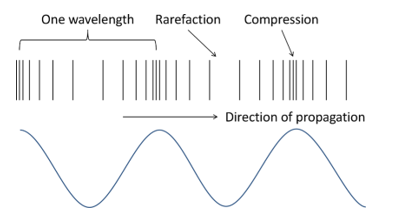
Sound waves propagate throughout the air, stretching out the air at some places and squeezing the air together at other places. These regions are called rarefactions and compressions respectively. As the sound wave moves, air is alternately stretched out and squeezed, many times per second. This is the frequency of the sound wave, measured in Hertz (Hz). If the sound wave stretches air 500 times and squeezes it 500 times per second, its frequency is 500 Hz. These vibrating air molecules collide against your eardrum, and you hear them as a musical note
Chapter 2: Development
So far, we have discussed what sounds are, and how we can hear them. But what makes sounds different from others? Why is listening to an orchestral performance pleasing and harmonious, while your neighbour singing in the shower is irritating and cacophonous? Let’s examine the frequencies of harmonious and cacophonous sounds.

(To listen to these frequencies, open two tabs of https://onlinetonegenerator.com/. Set the first tab to 1 and the second tab to Frequency 2, and click “Play” on both tabs)
It seems that as long as the ratio of the two frequencies is a rational number, then they are harmonious. 2:1 is harmonious, as well as 5:4. Conversely, if the ratio of the two frequencies is an irrational number, they will be cacophonous, such as √3:1 or π:1.
To test our theory, let us listen to some more frequencies:

It seems that our theory has been defeated, as 14:13 and 28:23 are both rational numbers, but produce cacophonous sounds. We need to modify our theory. Perhaps 2:1 and 5:4 are harmonious as their denominators are small, while 14:13 and 28:23 are cacophonous as their denominators are large. From this observation, we can come up with a new theory: Two frequencies are harmonious if the ratio of their frequencies is a rational number, with a small denominator in its reduced form.
Yet, musical instruments are rarely tuned such that the ratio of frequencies of two notes is a rational number with a small denominator. The most common tuning system today is known as equal-temperament, with the ratios of frequencies being successive twelfth-roots of 2:
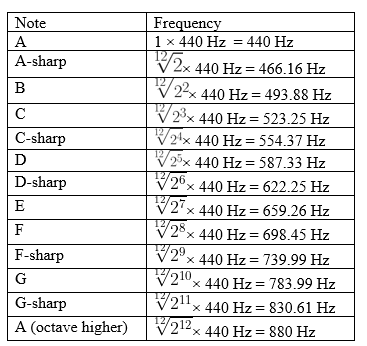
None of the ratios between two different notes are rational numbers. Yet, many pairs of frequencies still sound harmonious. Shostakovich’s Fugue in A Major, Op. 87 No.7 initially only uses the pitches A, C-sharp, and E, with frequencies of 440 Hz, 554.37 Hz, and 659.26 Hz respectively. Yet, it is one of the most harmonious musical pieces. Why is it so?
Upon closer examination, the frequencies involve closely approximate rational numbers with small denominators. 554:440 is approximately equal to 5:4, and 659:440 is also approximately equal to 3:2, within an error of 1%. Thus, one final change is required for our theory: Two frequencies are harmonious if the ratio of their frequencies is sufficiently close to a rational number, with a small denominator in its reduced form.
Chapter 3: Recapitulation
Musical instruments are tuned to successive twelfth-roots of 2 so that the ratio between two similar intervals is the same, thus ensuring overall harmony when different instruments play together. The octave is divided into twelve half-steps, with the frequencies of each half-step and their rational approximations shown below:
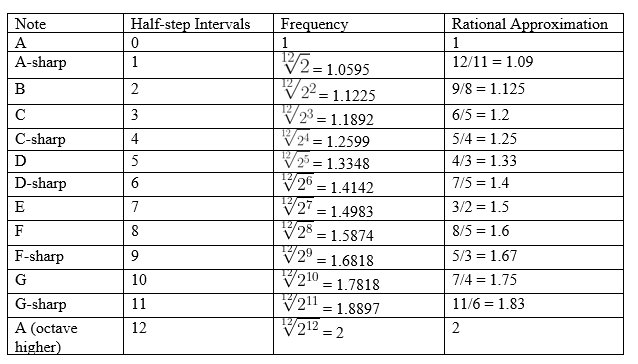
With an equal tuning system, the ratios between two intervals with the same number of half-steps will be the same. For example, from A to A (an octave higher), there are twelve half-steps. I can go from A to A directly, with the ratio of frequencies being 2, but I can also go from A to D-sharp, with six half-steps, and then from D-sharp to A, with six more half-steps. The resultant ratio would also be equal to 2.
However, if only rational numbers are used, then going from A to D-sharp would result in a ratio of 7/5. Going from D-sharp to A would result in a ratio of 7/5 again. Multiplying 7/5 by 7/5 gives 49/25 = 1.96. Adding intervals in this way will result in larger and larger numbers, eventually leading to more and more cacophonous sounds.
Both rational and irrational numbers can give rise to harmonious sounds, as well as cacophonous sounds. The modern system of tuning musical instruments makes it possible for multiple instruments to sound harmonious together, through approximating rational intervals with irrational numbers. The difference between the irrational intervals and their rational approximations are often too small for our sense of hearing to detect, and thus sound harmonious.
Test your Knowledge
1. At a busy intersection, a car sounds its horn with a frequency of 575 Hz. Another car also sounds its horn with a frequency of 725 Hz. Is the resulting pitch harmonious or cacophonous? Why?
Answers to Test your Knowledge
1. 725:575 is equal to 29:23. While it is a rational interval, it has a large denominator. However, 29/23 = 1.26, which is sufficiently close to 5/4 = 1.25. Thus the resulting pitch is harmonious.









