Chapter 1: The Scenario
Have you ever ordered Chicken McNuggets from McDonalds? Originally, Chicken McNuggets were only sold in boxes of 9 or 20 nuggets. It was soon discovered that you can buy certain numbers of Chicken McNuggets, but not other numbers. I cannot buy 88 Chicken McNuggets exactly, as there is no way to get 88 just by adding 9 and 20.
In the table below, the boxes shaded green contain numbers
of Chicken McNuggets that I can buy, while the white boxes contain numbers of Chicken McNuggets that I cannot buy.
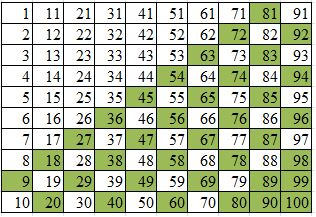
It seems that as the numbers increase, it is more likely that I can buy that number of Chicken McNuggets exactly. I can only buy one number from 1 to 10, but I can buy six of the numbers from 91 to 100. Is there a maximum number of Chicken McNuggets that I cannot buy?
Chapter 2: The Solution
In fact, if we continue the table for another 100 numbers, we find an interesting pattern: we can buy all numbers of Chicken McNuggets from 152 to 200.
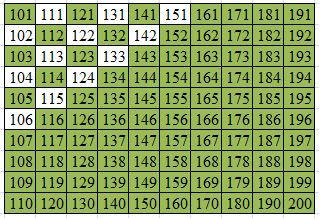
This poses the question: Is it possible to buy all numbers of Chicken McNuggets greater than 151? Even if I were to check every whole number from 151 to 10,000, and find out that it is possible to buy all of those numbers of Chicken McNuggets exactly, it is still not enough to prove that I can buy all possible numbers of Chicken McNuggets greater than 151. No matter
how far I check, there will always be numbers beyond that point which I cannot check. Thus, it is impossible to prove this just by checking alone. So how can I prove that 151 is the greatest number of Chicken McNuggets that I cannot buy? Let’s see how we can buy the first few numbers of Chicken McNuggets after that.
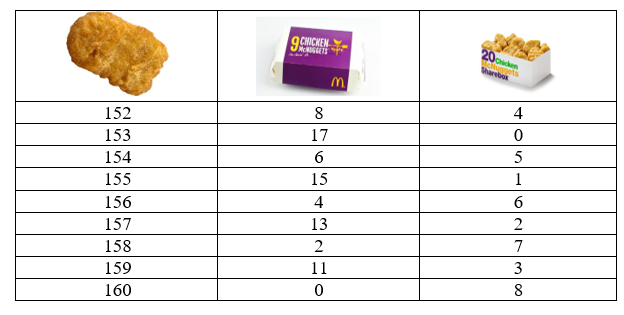
I can buy every number of Chicken McNuggets from 152 to 160!
But how can I use that to prove that all further numbers can be bought? Notice that if I want to buy 161 Chicken McNuggets, I can just buy 152 Chicken McNuggets first, then buy another box of 9. If I want to buy 162 Chicken McNuggets, I can buy 153 first, then another box of 9.
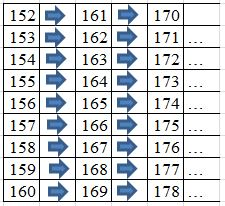
In this way, I can buy any number of Chicken McNuggets, as long as that number is greater than 151! Thus, we have proven that 151 is the greatest number of Chicken McNuggets that we cannot buy exactly.
Chapter 3: The General Case
We have shown that 151 nuggets is the greatest number of
Chicken McNuggets that we cannot buy exactly with boxes of 9 and 20 nuggets. What if the Chicken McNuggets come in different-sized boxes? After all, in some countries, Chicken McNuggets are sold in boxes of 4 and 9, or boxes of 6 and 20, and so on…
If there is a maximum number of Chicken McNuggets that I
cannot buy, it is important that the boxes must not have a common factor. For example, if Chicken McNuggets were sold in boxes of 4 and 6, then I could never buy any odd number of Chicken McNuggets, as there is no way I can make an odd number by adding 4 and 6. If Chicken McNuggets were sold in boxes of 6 and 9, I would never be able to buy any number of Chicken
McNuggets that is not a multiple of 3, as adding 6 and 9 would always result in a multiple of 3. Mathematicians call two numbers that have no common factors coprime. For example, 9 and 20 are coprime, as they share no common factors. 4 and 6 are not coprime, as they can both be divided by 2.
If Chicken McNuggets come in boxes of m and n, where m and n
are coprime whole numbers, the greatest number of Chicken McNuggets that I cannot buy is:
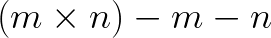
Using the example of boxes of 9 and 20 earlier, the greatest
number of Chicken McNuggets I cannot buy is: 9 × 20 – 9 – 20 = 180 – 29 = 151. This formula can be used widely in our daily lives. For example, if we only have $2 and $5 notes, what is the greatest amount of money that we cannot pay exactly? In Rugby, scoring a touchdown is worth 5 points and scoring a penalty is worth 3 points. What is the greatest number of points that cannot be scored?
Test your Knowledge
1. McDonalds sells chicken McNuggets in boxes of 9 and 20.
Can I buy 199 nuggets? If so, how can I do so?
2. Another fast-food restaurant sells chicken wings in boxes
of 5 and 8. What is the greatest number of chicken wings that I cannot buy from this fast-food restaurant?
3. Soft drinks are often sold in boxes of 6 and 24. Is there
a greatest number of soft drinks that cannot be bought? If there is, what is it? If not, why not?
4. Bob is playing a game with his friend. Hitting the target
gives 6 points, while hitting the bulls-eye gives 11 points instead. Bob likes to cheat by increasing his points when his friend isn’t looking. Currently, Bob has 49 points. What evidence is there that Bob has cheated?
Answers to Test your Knowledge
1. Using the Chicken McNugget Theorem, the greatest number
of Chicken McNuggets that cannot be bought is 9 × 20 – 9 – 20 = 151. Since 199 is greater than 151, it can be bought. One way is to buy 11 boxes of 9 nuggets, and 5 boxes of 20 nuggets.
2. Using the Chicken McNugget Theorem, the greatest number
of chicken wings that can be bought is 5 × 8 – 5 – 8 = 27.
3. The Chicken McNugget Theorem only works when the two
numbers involved are coprime. In this case, 6 and 24 are not coprime because they can both be divided by 6. Thus, I cannot buy any number of soft drinks that cannot be divided by 6, if I can only buy 6 or 24 cans at a time.
4. Using the Chicken McNugget Theorem, the greatest number
of points Bob cannot score is 6 × 11 – 6 – 11 = 49 points. Since Bob has 49 points, it can be said for sure that he cannot have obtained 49 points through playing normally, and thus he must have cheated.









